The Cayley Transform

---

The image below shows how the function g(z) = (z-i)/(z+i) maps the upper-half plane into the unit disk. Notice that the blue horizontal lines get mapped to the blue cirlces and the red vertical lines get mapped to the red circles (and line). Furthermore, the red curves always meet the blue curves at right angles.

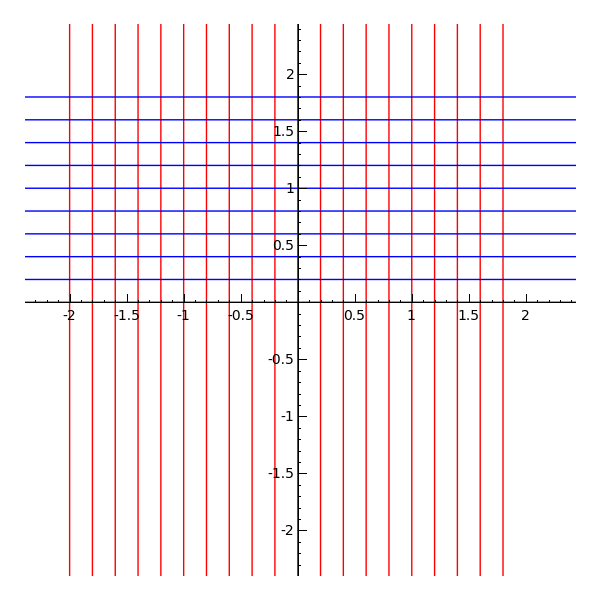g(z)     →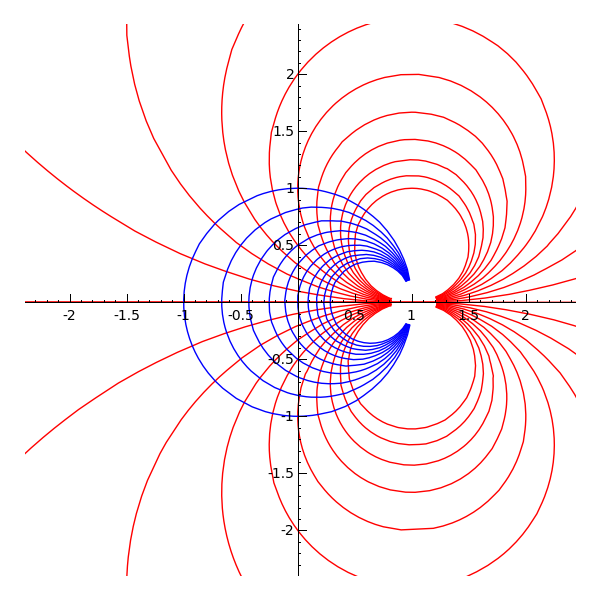

The Sage source code that generated the image on the right is given below:

var('z, t') size=2 A = Graphics() for k in range(-10,10):     #image of vertical lines     z=I*t+k/5 #parametrization for vertical lines     g = (z-I)/(z+I) #Cayley transform     A = A+parametric_plot((g.real(),g.imag()),-10,10,color='red') for k in range(0,10):     #image of horizonal lines     z=t+I*k/5 #parametrization for horizontal lines     g = (z-I)/(z+I) #Cayley transform     A = A+parametric_plot((g.real(),g.imag()),-10,10,color='blue') show(A,xmin=-size,xmax=size,ymin=-size,ymax=size,aspect_ratio=1)