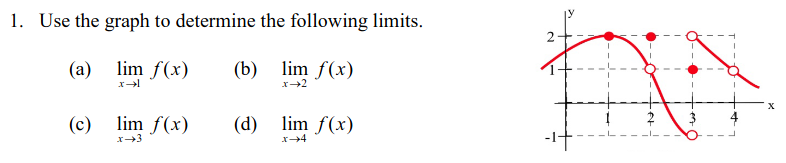
Today we focused on continuity. We talked about the three main types of discontinuities that graphs might have:
Here is a real world example of a jump discontinuity:
The limit of a function \(y = f(x)\) as \(x\) approaches \(a\) is the \(y\)-value that the graph appears to be heading towards. We use the notation \(\displaystyle \lim_{x \rightarrow a} f(x)\) to represent the limit. To calculate a limit, use the following steps:
First try plugging in \(a\) into the function. If \(f\) is continuous at \(a\), then the \(y\)-value you get is the answer.
If \(f(a)\) is undefined, try to simplify the function using algebra until you can calculate a value at \(a\). As soon as you get a number, you are done.
If \(f(x)\) is heading towards more than one y-value, then we say that the limit does not exist (DNE for short).
We did the following examples:
\(\displaystyle \lim_{x \rightarrow 2} \frac{x^2 - 3x +2}{x-2}\)
\(\displaystyle \lim_{x \rightarrow 3} \frac{x^2 - 3x +2}{x-2}\) (This time, \(x=3\) isn’t a bad point…)
\(\displaystyle \lim_{x \rightarrow 0} \frac{x-4}{x}\) (Notice that when you plug-in \(x=0\), you get a non-zero divided by zero…)
We finished by discussing one-sided limits. We did these two examples:
Think of \(0^-\) as a very tiny, but negative number. So the limit above is \(+\infty\). Try finding:
We started by reviewing limits. We did the following problems in class:
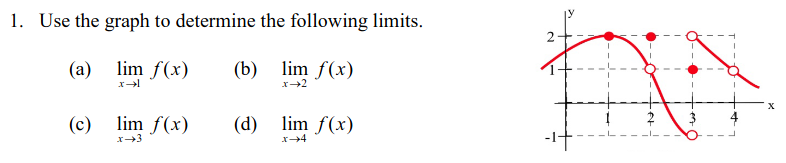
\(\displaystyle \lim_{x \rightarrow 2} \frac{x^2 - 4}{x-2}\) (Answer is 4)
\(\displaystyle \lim_{x \rightarrow 3^-} \frac{1}{(x-3)^2}\) (Answer is \(\infty\))
\(\displaystyle \lim_{x \rightarrow 1} \frac{x^2-1}{x^2 + 1}\) (Answer is 0)
Then we introduced the derivative of a function \(y = f(x)\). The derivative of \(f\) at \(x\) is two things:
We use several different notations to represent the derivative: \(f'(x)\), and \(y'\), and \(\dfrac{dy}{dx}\). These all mean the same thing.
To calculate the derivative, today we used the definition of the derivative: \[ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}.\] We did these two examples in class:
Use the definition of the derivative to find the derivative of \(f(x) = x^2\).
Use the definition of the derivative to find the derivative of \(y = x^3\).
Today we talked about easier ways to calculate derivatives. Here are three important rules. The symbol \(\dfrac{d}{dx}\) is shorthand that literally means “take the derivative with respect to \(x\).”
Power Rule. \(\dfrac{d}{dx} x^p = p x^{p-1}\).
Sum Rule. \(\dfrac{d}{dx} f(x) + g(x) = f'(x) + g'(x)\).
Constant Multiple Rule. \(\dfrac{d}{dx} c f(x) = c f'(x)\).
We used the power rule to differentiate \(x^5, \sqrt{x}\), and \(\dfrac{1}{x}\). Then we calculated the following examples in class:
Notice that the derivative of \(-4x\) is just \(-4\) since that is the slope of the line \(y= -4x\), and the derivative of any constant term like \(4\) is just zero.
Hint: Use algebra to find the combined power of \(x\) first.
Then we talked about the meaning of derivatives.
If a rock is dropped, it falls \(s\) feet in \(t\) seconds where \(s(t) = 16t^2\). Find the derivative \(s'(t)\). What are the units of the derivative and what does it represent?
Suppose it costs \(C(x) = 100 + \sqrt{x}\) dollars to make \(x\) golf balls. The marginal cost is the cost of making one more golf ball after producing \(x\) of them. It is approximately the same as the derivative \(C'(x)\). We calculated \(C'(x)\) and then used it to verify that \(C'(25)\) really is about the same as the cost of making one more golf ball after already having made 25.
Suppose that a town’s population will grow according to the formula \(P(t) = 4000 + 10t^3\), where \(t\) is measured in years from now. Find \(P'(t)\). What are the units of \(P'(t)\) and what does \(P'(t)\) represent?