Math 142 - Week 5 Notes

Monday, March 15

Today we introduced Integration by Parts. Here’s one video example of I-by-P. And here is another longer video with a good explanation. We did these in-class examples:

1. \(\displaystyle \int x \sin x \, dx\).

2. \(\displaystyle \int x^2 \ln x \, dx\).

3. \(\displaystyle \int \ln x \, dx\).

4. \(\displaystyle \int \arctan x \, dx\).

5. \(\displaystyle \int t^2 e^t \, dt\).

The last example requires integration by parts twice. An easier way to do integration by parts in this situation is tabular integration. We finished with one final tabular integration problem:

6. \(\displaystyle \int x^3 \cos(2x) \, dx\).

Here is a strange video of someone teaching the tabular method.

Wednesday, March 17

Today we talked about trigonometric integrals. Before starting, we did a classic tricky integration by parts problem. You can see a solution to this problem here.

1. \(\displaystyle \int e^x \cos x \, dx\).

Then we did several examples of trigonometric integrals. We followed the book pretty closely on this, so I’d recommend reading section 7.2. If you prefer videos, here’s a pretty good video explanation.

2. \(\displaystyle \int \cos^3 x \sin^2 x \, dx\)

3. \(\displaystyle \int \sin^3 x \, dx\)

4. \(\displaystyle \int \tan^6 x \sec^4 x \, dx\)

5. \(\displaystyle \int \tan^3 x \sec^7 x \, dx\). Hint: let \(u = \sec x\). Keep a \(\sec x \tan x\) factor to become the \(du\).

6. \(\displaystyle \int \frac{ \sec x}{\tan^2 x} \,dx\). Hint switch everything to sines and cosines first.

All of these problems could be solved with u-substitution and the two basic trig identities:

• \(\sin^2 x+ \cos^2 x = 1\) (This is the only identity you need to memorize!)
• \(\tan^2 x+ 1 = \sec^2 x\)

Then we talked about the trigonometric product identities:

• \(\cos(\alpha) \cos(\beta) = \tfrac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha - \beta)]\)
• \(\sin(\alpha) \sin(\beta) = \tfrac{1}{2}[\cos(\alpha-\beta)-\cos(\alpha + \beta)]\)
• \(\cos(\alpha) \sin(\beta) = \tfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha - \beta)]\)

A special case of the trig product identities are the half-angle formulas

• \(\cos^2 x = \frac{1}{2}+\frac{1}{2}\cos(2x)\)
• \(\sin^2 x = \frac{1}{2}-\frac{1}{2}\cos(2x)\)

We used these identities to evaluate:

7. \(\displaystyle \int \sin^2 x \, dx\).

8. \(\displaystyle \int \sin(8x) \cos(6x) \, dx\).

Friday, March 19

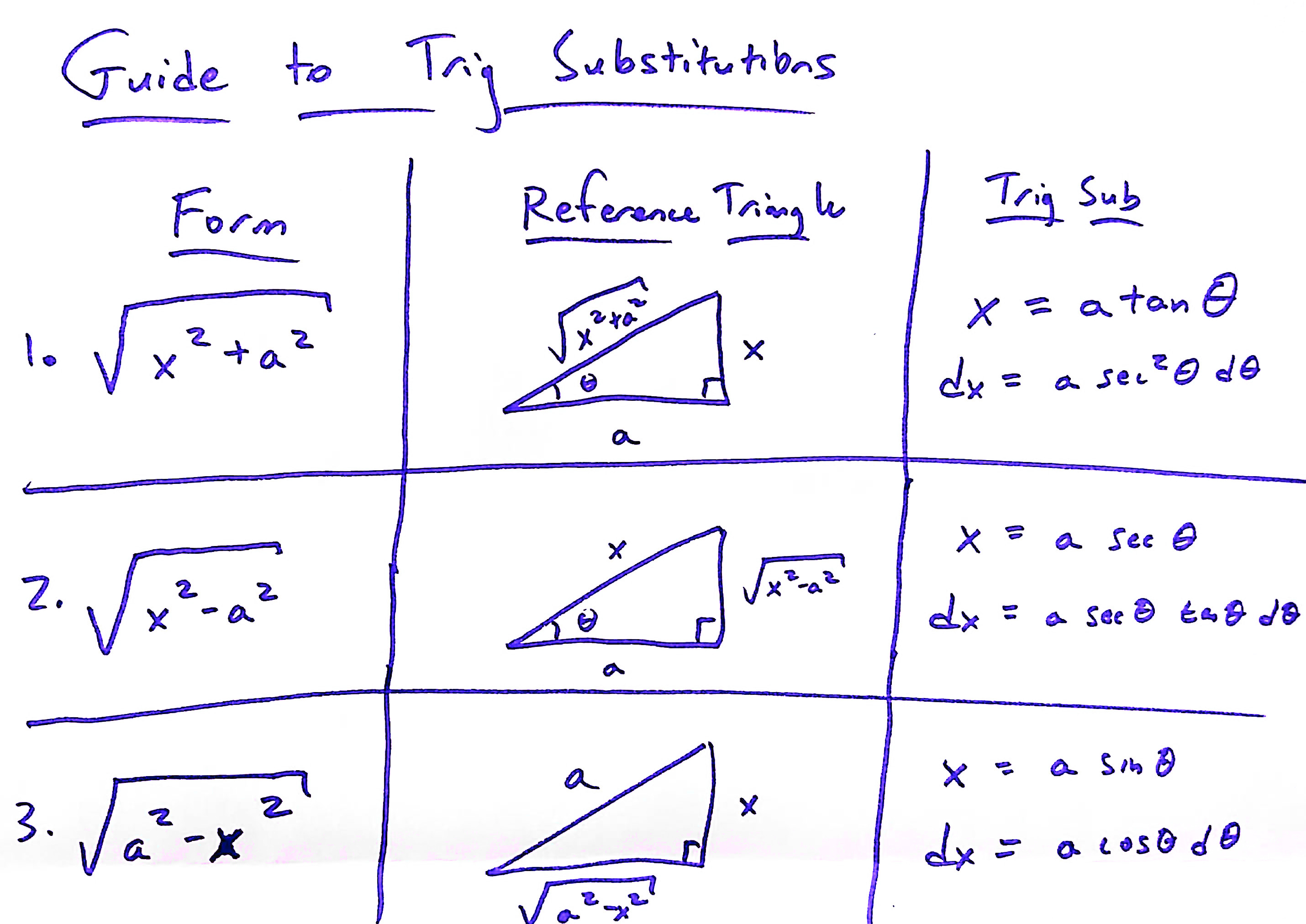
Today we introduced the idea of trigonometric substitutions. Here is a video example of the idea from Kahn academy:

We did the following examples in class:

1. \(\displaystyle \int \frac{dx}{(x^2+1)^{3/2}}\).

2. \(\displaystyle \int \frac{\sqrt{x^2-9}}{x} \, dx\).

3. \(\displaystyle \int \frac{x^2}{\sqrt{1-x^2}} \, dx\). (This integral comes up when you do I-by-P on \(\displaystyle \int x \arcsin x \, dx\))

4. \(\displaystyle \int \frac{1}{25+x^2} \, dx\).

In class, I made the following table with guidelines on how to make reference triangles based on the form of the function you are trying to integrate.