Babies Birthweight

The file babies.csv contains data on baby birthweights. The variables are:

• bwt - birth weight (in ounces)
• gestation - length of the pregnancy (in days)
• parity - 1 if baby was first born, 0 otherwise
• age - mother's age (in years)
• height - mother's height (in inches)
• weight - mother's weight (in lbs.)
• smoke - 1 if the mother is a smoker, 0 otherwise

babyData = read.csv('babies.csv')
head(babyData)
dim(babyData)

1. 1236
2. 8

Cleaning up the data

There are a lot of cells with NA (not available) entries, and these could mess up our analysis below. The na.omit() command is a fast way to remove these.

babyData = na.omit(babyData)
head(babyData)
dim(babyData)

1. 1174
2. 8

Checking the linear relationship

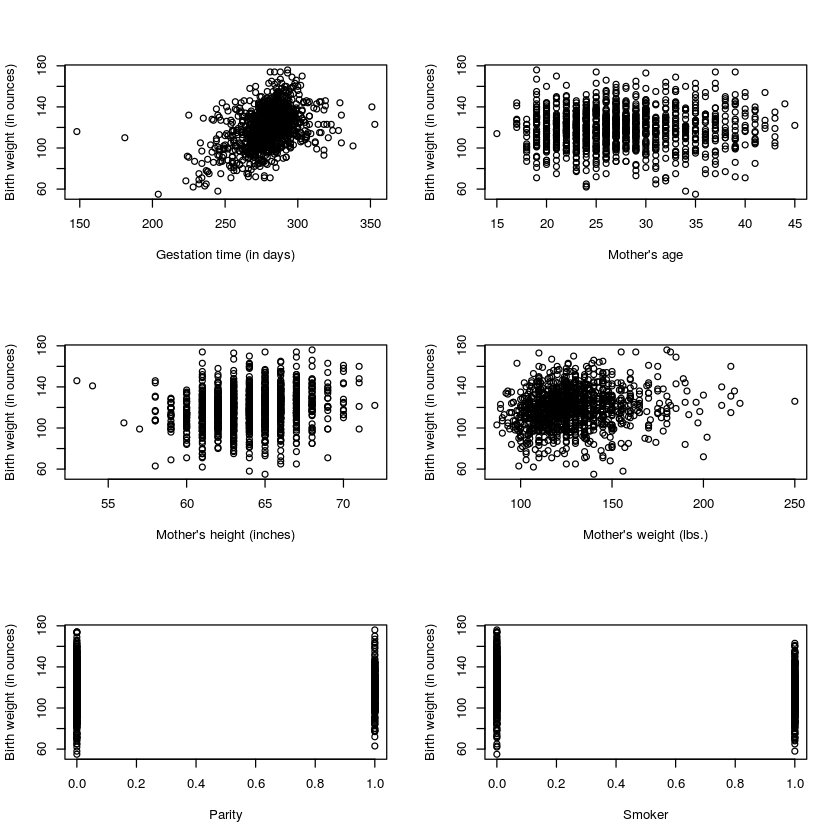
We need to check that there is a roughly linear relationship between each of the explanatory variables and the response variable. The par() command below lets us arrange the graphs in a 3-by-2 matrix.

par(mfrow=c(3,2))
plot(babyData$gestation,babyData$bwt,xlab='Gestation time (in days)',ylab='Birth weight (in ounces)')
plot(babyData$age,babyData$bwt,xlab="Mother's age",ylab='Birth weight (in ounces)')
plot(babyData$height,babyData$bwt,xlab="Mother's height (inches)",ylab='Birth weight (in ounces)')
plot(babyData$weight,babyData$bwt,xlab="Mother's weight (lbs.)",ylab='Birth weight (in ounces)')
plot(babyData$parity,babyData$bwt,xlab="Parity",ylab='Birth weight (in ounces)')
plot(babyData$smoke,babyData$bwt,xlab="Smoker",ylab='Birth weight (in ounces)')

Checking the residuals

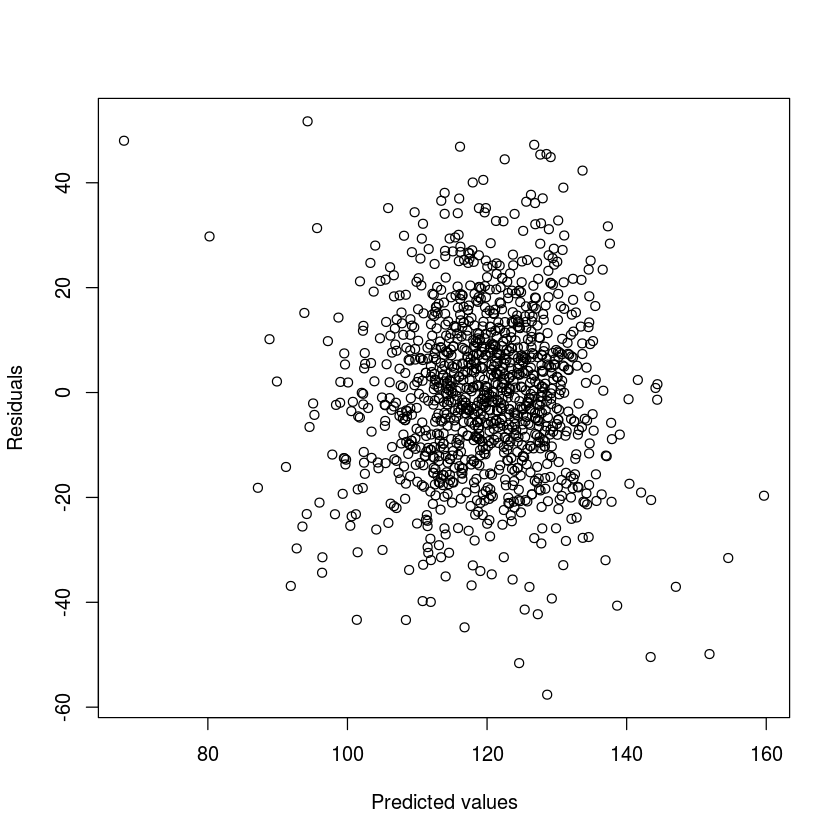
Just like in single variable regression, we need to check the residuals to see that they are roughly normally distributed with the same variance. This is much harder to do with so many variables. So here are some of the most important cases to check:

• residuals -vs- predicted values (\(\hat{y}\))
• residuals -vs- each explanatory variable
• A normal quantile plot of residuals (to check for normality)

myLM = lm(bwt~gestation+age+height+weight+parity+smoke,data=babyData)

qqnorm(resid(myLM))
plot(fitted(myLM),resid(myLM),xlab='Predicted values',ylab='Residuals')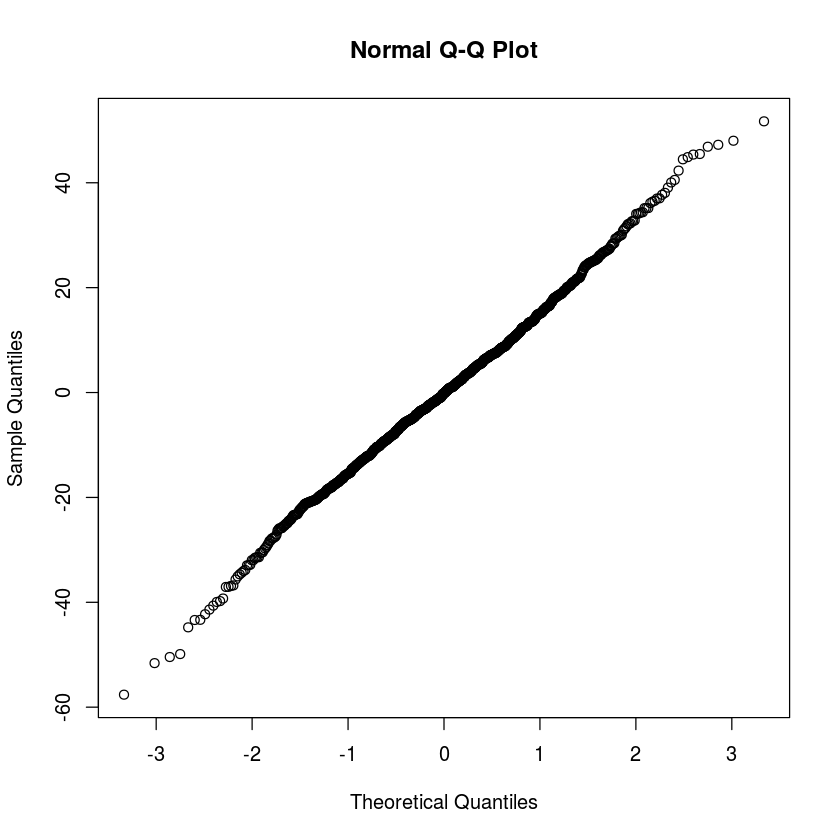

par(mfrow=c(3,2))
plot(babyData$gestation,resid(myLM),xlab='Gestation time (in days)',ylab='Residuals')
plot(babyData$age,resid(myLM),xlab="Mother's age",ylab='Residuals')
plot(babyData$height,resid(myLM),xlab="Mother's height (inches)",ylab='Residuals')
plot(babyData$weight,resid(myLM),xlab="Mother's weight (lbs.)",ylab='Residuals')
plot(babyData$parity,resid(myLM),xlab="Parity",ylab='Residuals')
plot(babyData$smoke,resid(myLM),xlab="Smoker",ylab='Residuals')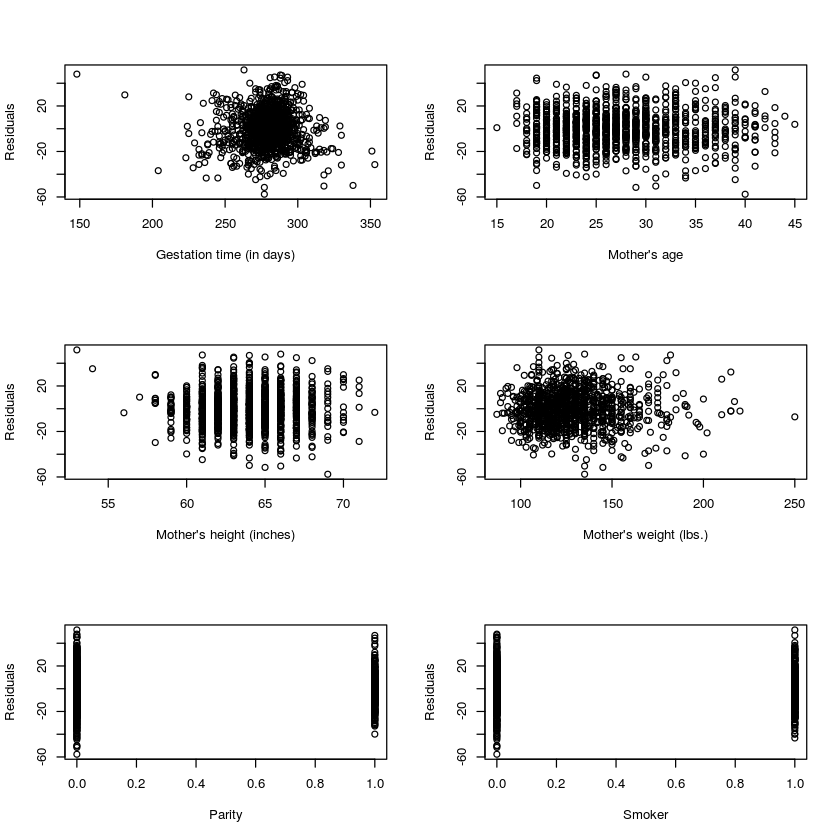

The residuals mostly seem to have the same variance throughout, there is not clear trend in the scatterplots above. The qq-plot make it clear that the residuals are very normal, which is good.

summary(myLM)

Call:
lm(formula = bwt ~ gestation + age + height + weight + parity + 
    smoke, data = babyData)

Residuals:
    Min      1Q  Median      3Q     Max 
-57.613 -10.189  -0.135   9.683  51.713 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -80.41085   14.34657  -5.605 2.60e-08 ***
gestation     0.44398    0.02910  15.258  < 2e-16 ***
age          -0.00895    0.08582  -0.104  0.91696    
height        1.15402    0.20502   5.629 2.27e-08 ***
weight        0.05017    0.02524   1.987  0.04711 *  
parity       -3.32720    1.12895  -2.947  0.00327 ** 
smoke        -8.40073    0.95382  -8.807  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 15.83 on 1167 degrees of freedom
Multiple R-squared:  0.258, Adjusted R-squared:  0.2541 
F-statistic: 67.61 on 6 and 1167 DF,  p-value: < 2.2e-16

Choosing the best model

We will now remove variables from the full model to get the model with the best adjusted R-squared.

adjustedLM = lm(bwt~gestation+height+weight+parity+smoke,data=babyData)
summary(adjustedLM)

Call:
lm(formula = bwt ~ gestation + height + weight + parity + smoke, 
    data = babyData)

Residuals:
    Min      1Q  Median      3Q     Max 
-57.716 -10.150  -0.159   9.689  51.620 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -80.71321   14.04465  -5.747 1.16e-08 ***
gestation     0.44408    0.02907  15.276  < 2e-16 ***
height        1.15497    0.20473   5.641 2.11e-08 ***
weight        0.04983    0.02503   1.991  0.04672 *  
parity       -3.28762    1.06281  -3.093  0.00203 ** 
smoke        -8.39390    0.95117  -8.825  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 15.82 on 1168 degrees of freedom
Multiple R-squared:  0.2579,    Adjusted R-squared:  0.2548 
F-statistic:  81.2 on 5 and 1168 DF,  p-value: < 2.2e-16

Prediction intervals and confidence intervals for parameters

These work exactly the same as the single variable case.

confint(adjustedLM)

predict(adjustedLM,data.frame(gestation = 240,height=70,weight=120,age=25,parity=1,smoke=0),interval='prediction')