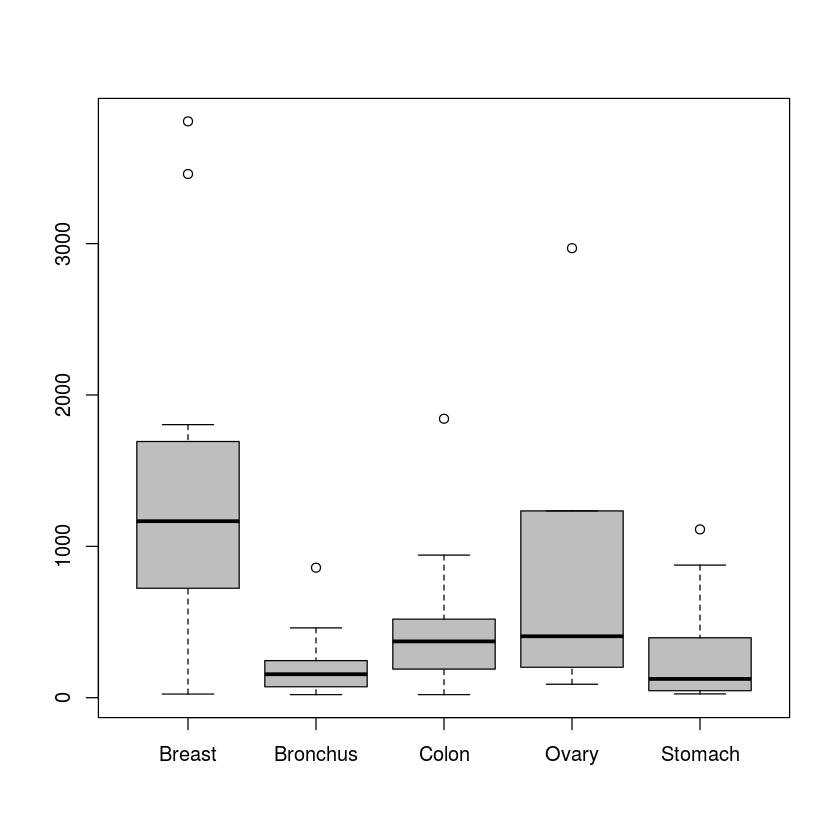
In the 1970s, doctors wondered if giving terminal cancer patients a supplement of ascorbate would prolong their lives. They designed an experiment to compare cancer patients who received ascorbate to cancer patients who did not receive the supplement. The result of that experiment was that, in fact, ascorbate did seem to prolong the lives of these patients. But was the effect of ascorbate different when different organs were affected by the cancer? The file CancerSurvival.CSV contains data about the survival times of these patients (in days). The data is only for the patients who received the ascorbate supplement.
survivalData=read.csv('CancerSurvival.CSV')boxplot(survivalData$Survival~survivalData$Organ,col='gray')
summaryTable = function(xcol,ycol,DF) {
# Returns a matrix showing sample size, mean, and std. dev. for each group.
# xcol is the column number of the groups, ycol is the column number of the quantitative response variable, DF is the dataframe.
N = as.matrix(summary(DF[[xcol]]))
M = as.matrix(aggregate(DF[[ycol]]~DF[[xcol]],DF,mean))[,2]
S = as.matrix(aggregate(DF[[ycol]]~DF[[xcol]],DF,sd))[,2]
A = cbind(N,M,S)
colnames(A) = c('Sample Size','Mean','Std. Dev.')
A
}
summaryTable(2,1,survivalData)| Sample Size | Mean | Std. Dev. | |
|---|---|---|---|
| Breast | 11 | 1395.9091 | 1238.9667 |
| Bronchus | 17 | 211.5882 | 209.8586 |
| Colon | 17 | 457.4118 | 427.1686 |
| Ovary | 6 | 884.3333 | 1098.5788 |
| Stomach | 13 | 286.0000 | 346.3096 |
myAOV = aov(Survival~Organ,survivalData)
qqnorm(resid(myAOV))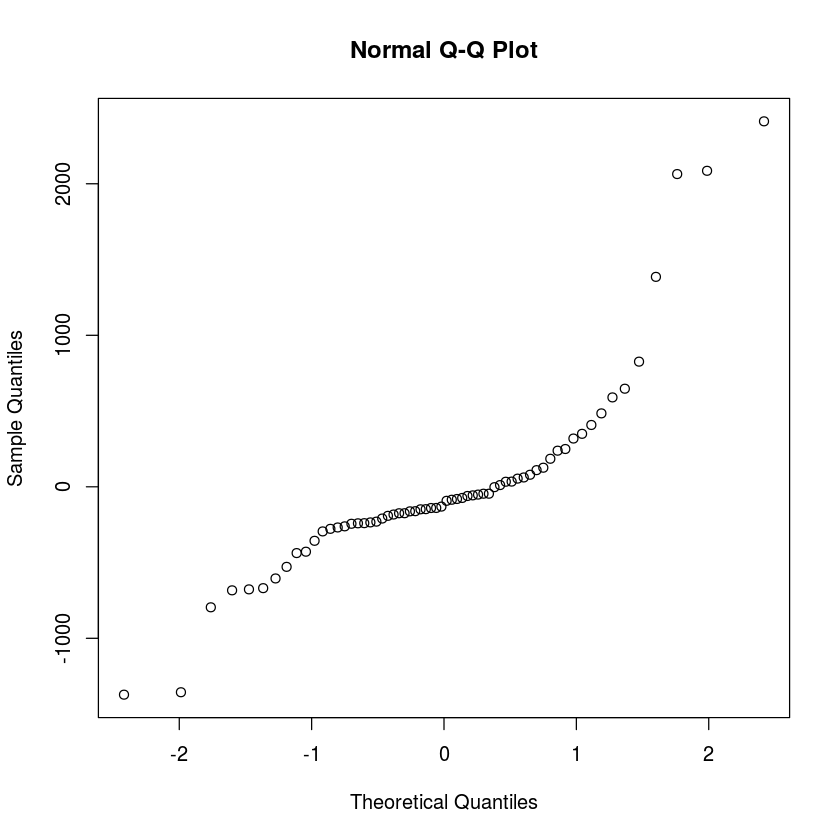
Both the assumption of constant variance, and the assumption of normal residuals are clearly not satisfied, so it is not a good idea to do ANOVA on this data. But we can safely do the Kruskal-Wallis test to see if the data have statistically significant differences in their medians (we just have to assume that each kind of cancer has a different median survival time, but with roughly the same shape probability distribution for the data).
kruskal.test(Survival~Organ,survivalData) Kruskal-Wallis rank sum test
data: Survival by Organ
Kruskal-Wallis chi-squared = 14.954, df = 4, p-value = 0.004798