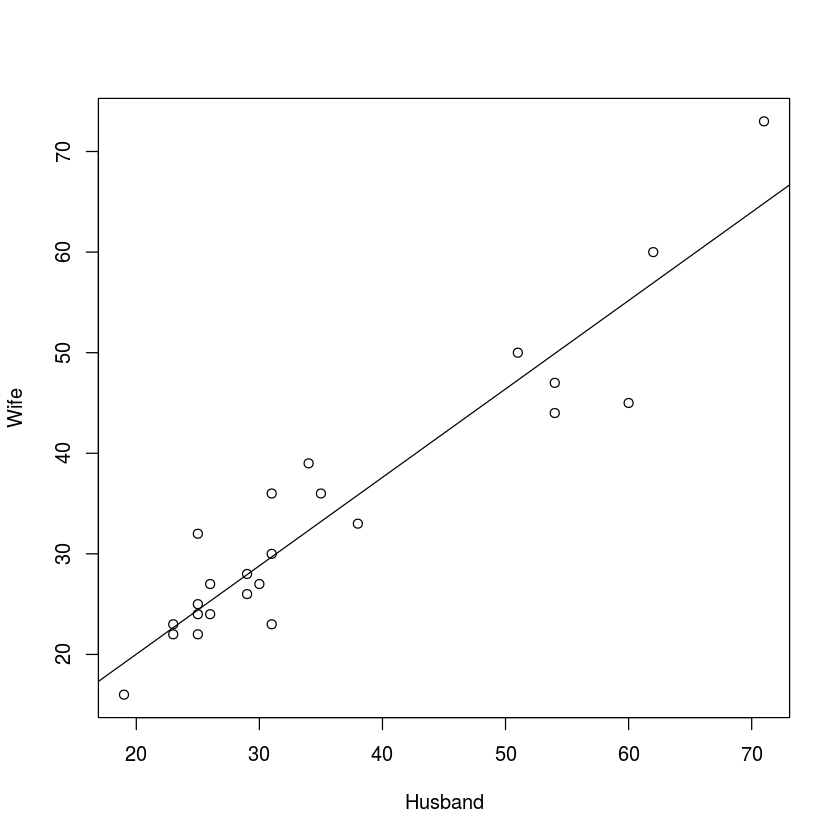
myData = read.csv("marriageAges.csv")plot(myData)
abline(lm(myData$Wife~myData$Husband))
From the scatterplot above, we can tell that the data has a linear relationship.
myLM = lm(myData$Wife~myData$Husband)
plot(myData$Husband,resid(myLM))
abline(0,0)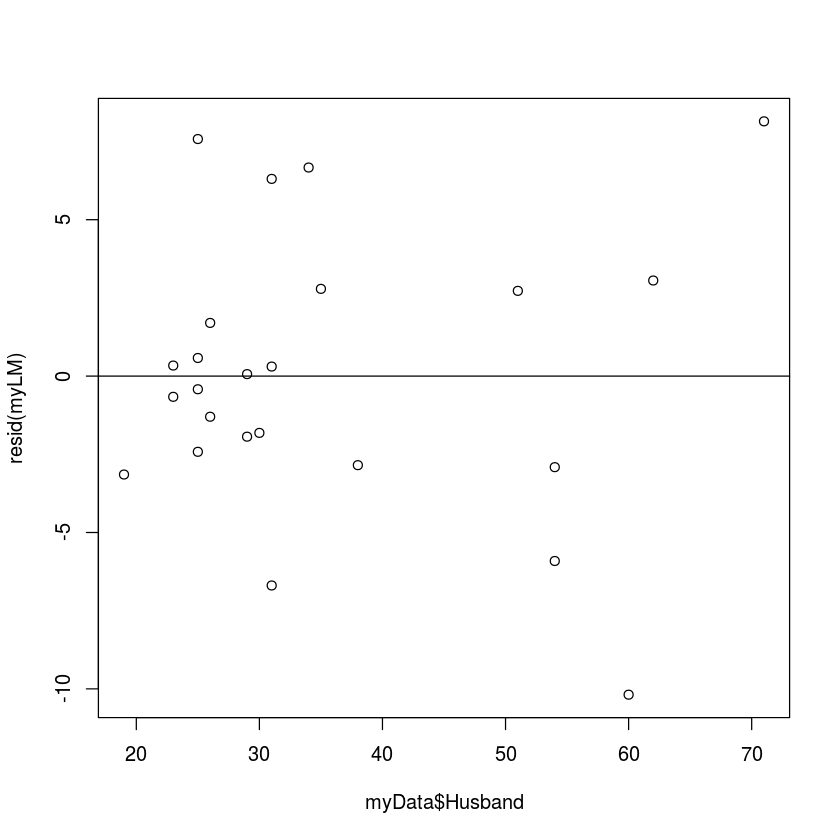
The residual plot makes it clear that the standard deviation of the residuals doesn't seem to depend on the x-values. The residuals seem to have pretty much the same distribution regardless of the husband's age. The residuals for older men might be a little more variable, but not by much.
qqnorm(resid(myLM))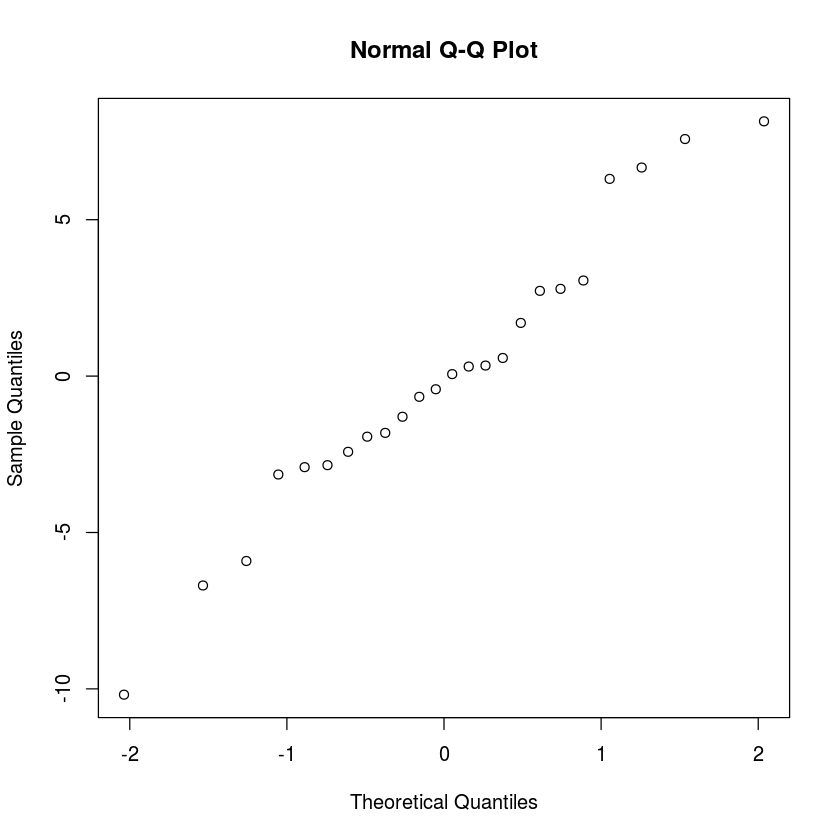
From the normal quantile plot, it is clear that the data is normal.
class(myLM)'lm'
Notice that myLM has class 'lm', which means that R thinks that it is a linear model.
confint(myLM,level=0.9)| 5 % | 95 % | |
|---|---|---|
| (Intercept) | -1.882864 | 6.774472 |
| myData$Husband | 0.7664140 | 0.9915807 |
The confint() command takes a linear model and gives confidence intervals for the slope and y-intercept.
# Use the same variable x as in the model.
x = myData$Husband
y = myData$Wife
predict(lm(y~x),data.frame(x=60),interval='prediction')| fit | lwr | upr | |
|---|---|---|---|
| 1 | 55.18564 | 44.94681 | 65.42448 |
The predict() command can be used to make confidence intervals for the mean y-value at a particular x-value. It can also make prediction intervals as in the example above. Make sure you understand the difference between the two types of intervals.
## Prediction Intervals vs. Confidence Intervals
new <- data.frame(x = c(20,45,70))
pred.w.plim <- predict(lm(y ~ x), new, interval = "prediction")
pred.w.clim <- predict(lm(y ~ x), new, interval = "confidence")
matplot(new$x, cbind(pred.w.clim, pred.w.plim[,-1]),
lty = c(1,2,2,3,3), type = "l", ylab = "predicted y")
The figure above shows the difference between confidence intervals for the regression line (inner green and red dashed lines) versus prediction intervals (outer blus dotted lines.)