Do phone companies take longer to service their competitors' customers than their own? The data below list the time (in hours) that it takes Verizon to fix problems with their phone lines. The groups are Verizon customers (ILEC) and competitor customers (CLEC). The question is, how much longer does Verizon take to fix its own customers' problems than those of its competitors' customers.
serviceData = read.csv("phoneService.csv")head(serviceData)| Time | Group | |
|---|---|---|
| 1 | 17.5 | ILEC |
| 2 | 2.4 | ILEC |
| 3 | 0 | ILEC |
| 4 | 0.65 | ILEC |
| 5 | 22.23 | ILEC |
| 6 | 1.2 | ILEC |
estimate=mean(subset(serviceData,Group=='ILEC')$Time)-mean(subset(serviceData,Group=='CLEC')$Time)hist(serviceData$Time,col='gray')
differences = c()
for (i in 1:5000) {
verizonMean = mean(sample(subset(serviceData,Group=='ILEC')$Time,replace=TRUE))
CLECMean = mean(sample(subset(serviceData,Group=='CLEC')$Time,replace=TRUE))
difference = verizonMean-CLECMean
differences = c(differences,difference)
}hist(differences,col='gray')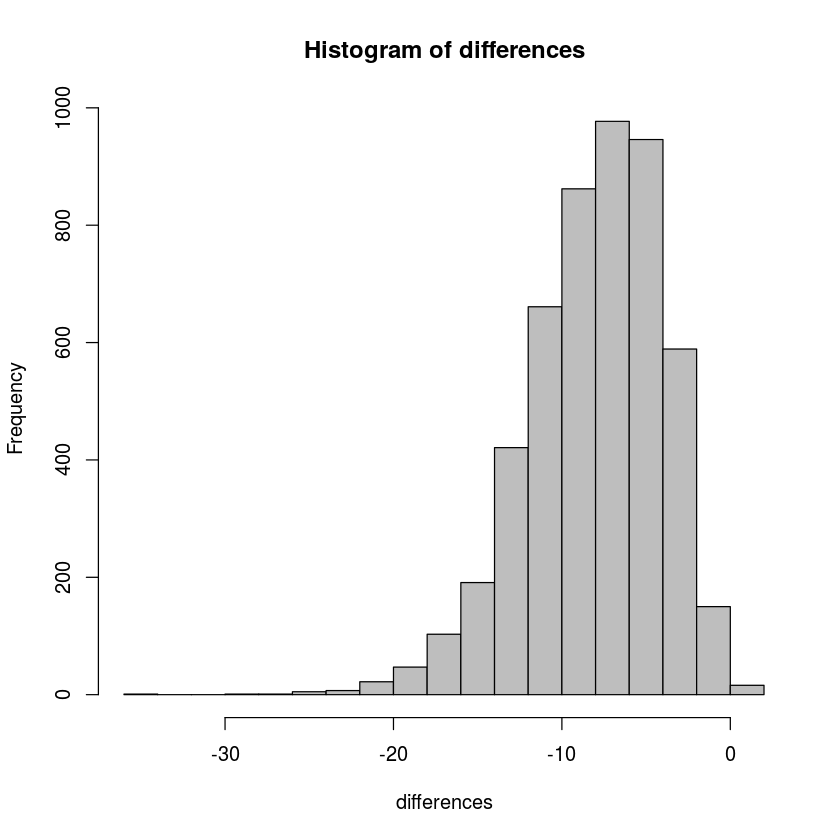
quantile(differences,0.025)
quantile(differences,0.975)2.5%: -16.8977244591346
97.5%: -1.66385246394231
2*estimate-quantile(differences,0.975)
2*estimate-quantile(differences,0.025)97.5%: -14.5311872517767
2.5%: 0.702684743415553
The second confidence interval is much better than the first, because it corrects for the skew in the bootstrap distribution. It also makes it clear that we cannot be sure there is a statistically significant difference between the Verizon customers and the competitor customers, since zero is in the confidence interval. That is an important difference.