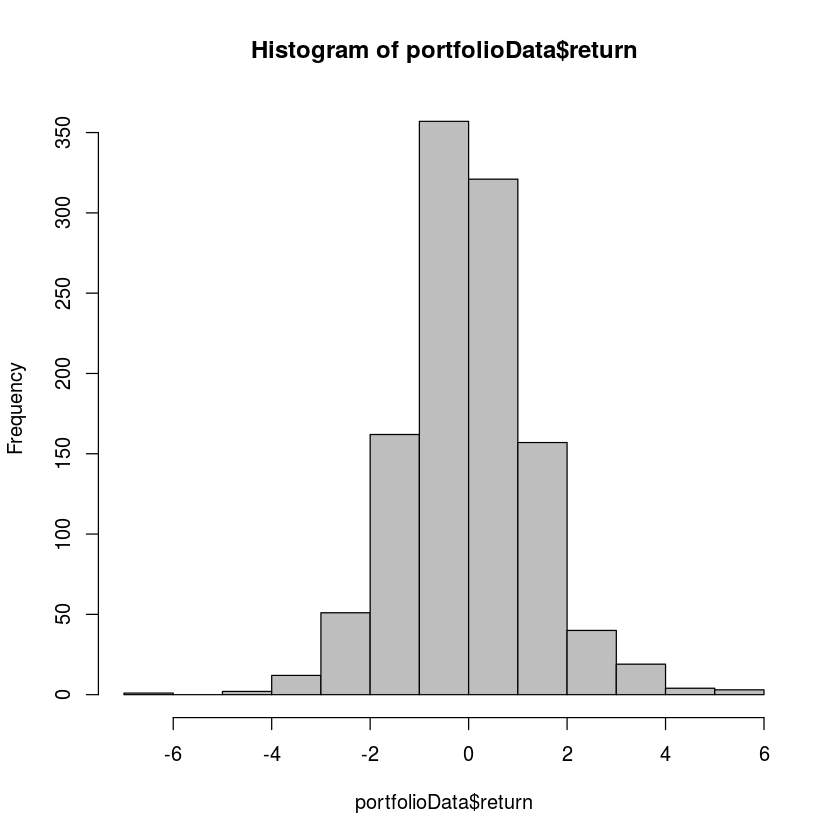
In financial theory, the standard deviation of returns on an investment is one way to measure the risk of the investment. The idea is that investment with highly variable returns are riskier than investments with returns that are always the same. The data file Portfolio.csv contains the returns (in percent) on 1129 consecutive days for one stock market portfolio. We will use bootstrapping to estimate the standard deviation (and therefore the risk) for this portfolio.

portfolioData = read.csv("Portfolio.csv")
head(portfolioData)
return
1 0.229
2 0.936
3 -0.646
4 -0.858
5 -1.44
6 0.182 
sd(portfolioData$return)

1.3247529510227

hist(portfolioData$return,col='gray')

To get the bootstrap distribution for standard deviation, we will collect 5000 bootstrap samples and compute the standard deviation for each.

sdResults = c()
for (i in 1:5000) {
    sdResults = c(sdResults,sd(sample(portfolioData$return,replace=TRUE)))
}
hist(sdResults,col='gray')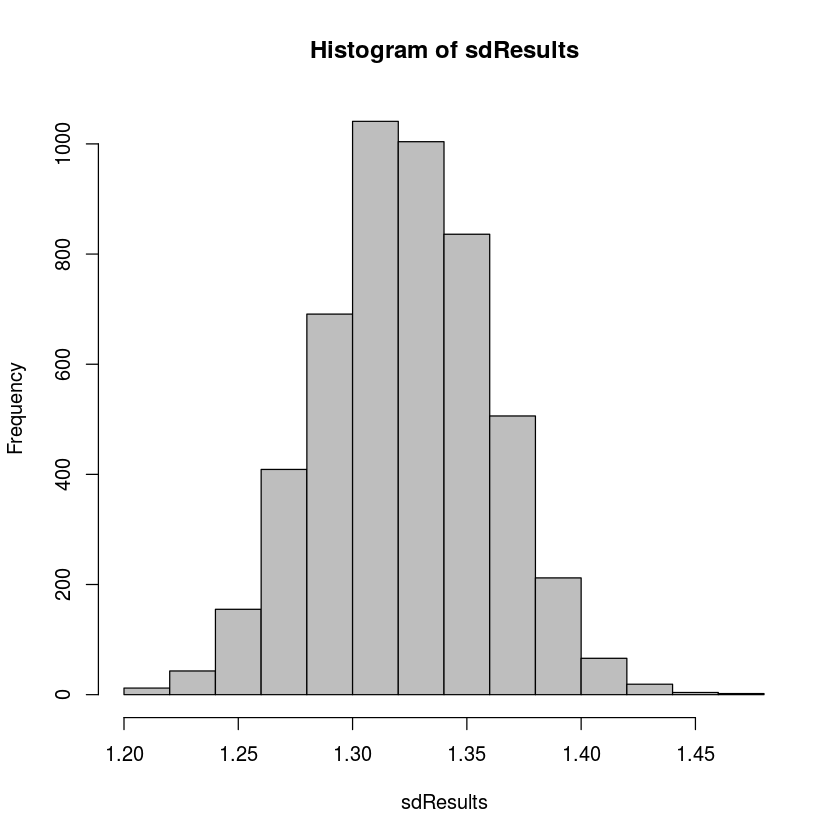

Like all bootstrap distributions, this distribution has the following important features:

  1. Shape - Is it skewed left/right? Is it approximately normal?
  2. Center - The center (mean) of the bootstrap distribution is the estimate for the population parameter you are interested in (assuming that the sample statistic is an unbiased estimator of the population parameter). In fact, if the sample statistic is a mathematically biased estimator (like the population standard deviation formula), then bootstrap can actually estimate how bad the bias is by computing the difference between the mean of the bootstrap distribution and the value of the statistic calculated from the original sample.
  3. Spread - The standard deviation of the bootstrap distribution can be used, for example, to make t-distribution confidence intervals for the population parameter if the bootstrap distribution is roughly normal.

The estimate for the population standard deviation is:

mean(sdResults)

1.32339647051005

An estimate for the mathematical bias is:

mean(sdResults)-sd(portfolioData$return)

-0.00135648051265047

This bias term above is three orders of magnitude smaller than the estimate for the parameter, so the sample standard deviation appears to be an unbiased estimator for the population parameter.

qqnorm(sdResults)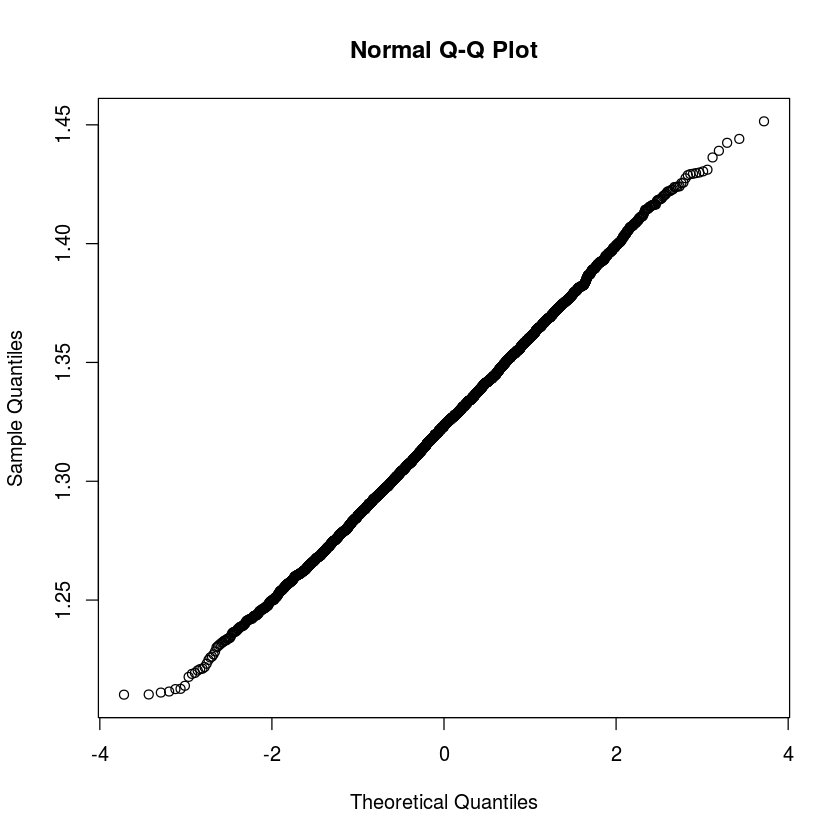
 sd(sdResults)

0.0373263086654002

mean(sdResults)-1.962*sd(sdResults)
mean(sdResults)+1.962*sd(sdResults)

1.24987507318962

1.39634350839265

quantile(sdResults,0.025)
quantile(sdResults,0.975)

2.5%: 1.25104406408997

97.5%: 1.39736414865592

As you can see, the t-distribution based confidence interval is very similar to the quantile based one.