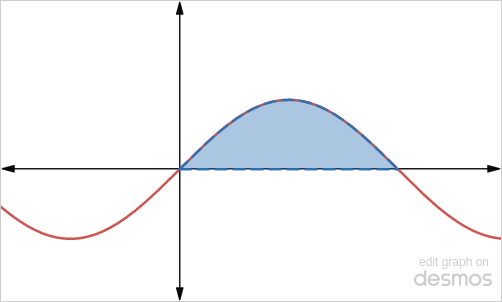
The function is a wave. How much area is under one arch of the sine wave?
Find the indefinite integral .
Jump to week:
| Day | Section | Topic |
|---|---|---|
| Mon, Aug 21 | 5.4 | The indefinite integral and substitutions |
| Wed, Aug 23 | 5.5 | The definite integral |
| Thu, Aug 24 | Review | |
| Fri, Aug 25 | 5.8 | Numerical integration |
We started by reviewing integration. We did the following exercises.
The function is a wave. How much area is under one arch of the sine wave?

Find the indefinite integral .
Then we introduced integration by substitution (see page 198 in the textbook).
(Hint: you don’t have to use substitution for this one, but substitution will work too.)
Today, we started by reviewing the product rule & chain rule for derivatives with these two examples:
Then we did more integrals using u-substitution:
3. (https://youtu.be/jSa5z2HIQ6U)
Today we went over Homework 1. We also looked at this sheet about how to approach integral problems:
Today we talked about even and odd functions and how they are sometimes easier to integrate than other functions:
.
We also talked about how to use Riemann sums:
where
We did the following example:
| Day | Section | Topic |
|---|---|---|
| Mon, Aug 28 | 6.4 | The natural logarithm function (derivatives) |
| Wed, Aug 30 | 6.4 | The natural logarithm function (integrals) |
| Thu, Aug 31 | 6.2 | The exponential ex |
| Fri, Sep 1 | 4.3 | Inverse functions and their derivatives |
The natural logarithm function is defined We looked at this definition and used it to make a list of the important properties of the natural logarithm. Then we did these examples of derivatives involving the natural logarithm.
Differentiate . (https://youtu.be/Fa2IlTP4hxM)
.
.
We also talked about logarithmic differentiation. We did this example:
On Wednesday, we talked about integrals involving natural logarithms. But first, we did a warm-up logarithmic differentiation problem.
Use logarithmic differentiation to find the derivative of .
(Don’t forget the absolute values since !)
Compare these two integrals: and . Which answer involves a natural logarithm and which doesn’t?
Today we went over Homework 2. We also introduced the natural exponential function ex and did the following problems in class:
.
.
Today we talked about inverse trig functions. We derived formulas for their derivatives, which can be found on the (formula sheet) for the exams. We also used reference triangles to help calculate values from inverse trig functions.
Evaluate .
Find . (https://youtu.be/gNdEV_QfFIw)
Find the derivative of . (https://youtu.be/qrLOB1eanTE)
| Day | Section | Topic |
|---|---|---|
| Wed, Sep 6 | 6.4 | Inverse trigonometric functions |
| Thu, Sep 7 | Review | |
| Fri, Sep 8 | 6.1 | Exponentials and logarithms |
Today we did more examples with inverse trigonometric functions.
Simplify . (https://youtu.be/IxmrK1mwk5c)
.
.
Find the max of .
Today we talked about logarithms to other bases. We did these examples:
Compute without a calculator.
Simplify .
Solve .
Solve .
Today we derived the change of base formulas:
Simplify
If the population of a town grows at 6% per year, how long until the population doubles?
Here is a cool video with a nice trick to estimate the answer to the last problem:
We finished by talking about the rule of 70, which is a way to estimate the solution of when is constant percentage and is an unknown amount of time.
| Day | Section | Topic |
|---|---|---|
| Mon, Sep 11 | 6.3 | Differential equations & slope fields |
| Wed, Sep 13 | 6.5 | Separable equations |
| Thu, Sep 14 | Review | |
| Fri, Sep 15 | Midterm 1 |
Today we introduced differential equations. A differential equation is an equation with a derivative or differentials in it.
For some (simple) differential equations you can separate the variables (see section 6.5 in the textbook) and then integrate. We also talked about how you can graph a differential equation by plotting the slope field (see Slope Field Grapher). This lead to two key ideas:
Idea 1. A solution of a differential equation is a function, not a number. Every differential equation has infinitely many different solutions.
Idea 2. The solution functions all follow the slope field.
We did several examples:
Solve . (https://youtu.be/8Amgakx5aII)
Solve .
We also pointed out that separation of variables doesn’t always work, but you can still say something about the solutions using the slope field:
There is a tool on the software tab to plot slope fields. We finished with this example:
Today we started with a question about logarithms:
This led to a short discussion of what logarithms represent and why they are so useful. Then we talked about how to solve initial value problems by using an initial condition to solve for the constant in the general solution of a differential equation. We did the following in class:
Show that is a solution to for any . Then solve the initial value problem with initial condition .
with . (https://youtu.be/cc3qtMBdQlE)
Exponential growth (and decay) In English, this differential equation literally means the rate of growth of a population is directly proportional to the size of the population. The constant is called the proportionality constant.
Explosion equation . This equation models a chemical reaction where the rate of growth of a product of a reaction is directly proportional to the amount of the product squared. When we solved this equation, we saw that it leads to infinite growth in a finite amount of time!
| Day | Section | Topic |
|---|---|---|
| Mon, Sep 18 | 6.5 | Applications of differential equations |
| Wed, Sep 20 | 6.6 | Euler’s method |
| Thu, Sep 21 | Review | |
| Fri, Sep 22 | 7.1 | Integration by parts |
Today we started with this example:
Newton’s law of cooling says that the rate of change of the temperature of a small object is directly proportional to the difference between the objects temperature and the temperature of the surroundings .
Find the proportionality constant in the solution of Newton’s law of cooling if a cup of coffee is initially C and is 40C after 10 minutes in a room that is C.
Then we did this activity in class:
Today we finished talking about differential equations by introducing Euler’s method which is based on the simple observation that if , then Euler’s method has two parts:
Setup: Let and be the values from the initial condition, and choose a step size .
Recursive step: Repeatedly update and then using the formulas until you reach the desired location.
Here is a Kahn Academy Video (https://youtu.be/q87L9R9v274) if you would like a different explanation of Euler’s method and here is example computer code that we used in class:
We looked at the following examples:
with initial condition and step size .
with initial condition and step size .
with initial condition and step size .
with initial condition and step size . This is an example of the Logistic Equation.
Today we introduced Integration by Parts. Here is a longer video with a good explanation. We did these in-class examples:
.
.
.
The last example requires integration by parts twice. An easier way to do integration by parts in this situation is tabular integration. We finished with one final tabular integration problem:
Here is a strange video of someone teaching the tabular method.
| Day | Section | Topic |
|---|---|---|
| Mon, Sep 25 | 7.1 | Integration by parts - con’d |
| Wed, Sep 27 | 7.2 | Trigonometric integrals |
| Thu, Sep 28 | Review | |
| Fri, Sep 29 | 7.3 | Trigonometric substitutions |
Today we did more examples of integration by parts.
.
.
Today we did several examples of trigonometric integrals. We followed the book pretty closely on this, so I’d recommend reading section 7.2.
. Hint: let . Keep a factor to become the .
. Hint switch everything to sines and cosines first.
All of these problems could be solved with u-substitution and the two basic trig identities:
Today we reviewed homework 6. We also talked about which functions make better u’s and which functions make better dv’s in integration-by-parts. We did one extra example in class using the half-angle formulas from the formula sheet:
Today we talked about trigonometric substitutions. We did the following examples:
| Day | Section | Topic |
|---|---|---|
| Mon, Oct 2 | 7.4 | Partial fractions |
| Wed, Oct 4 | 7.4 | Partial fractions - con’d |
| Thu, Oct 5 | Review | |
| Fri, Oct 6 | 3.8 | L’Hospital’s rule |
Here is a table which summarizes all of the possible trig substitutions:
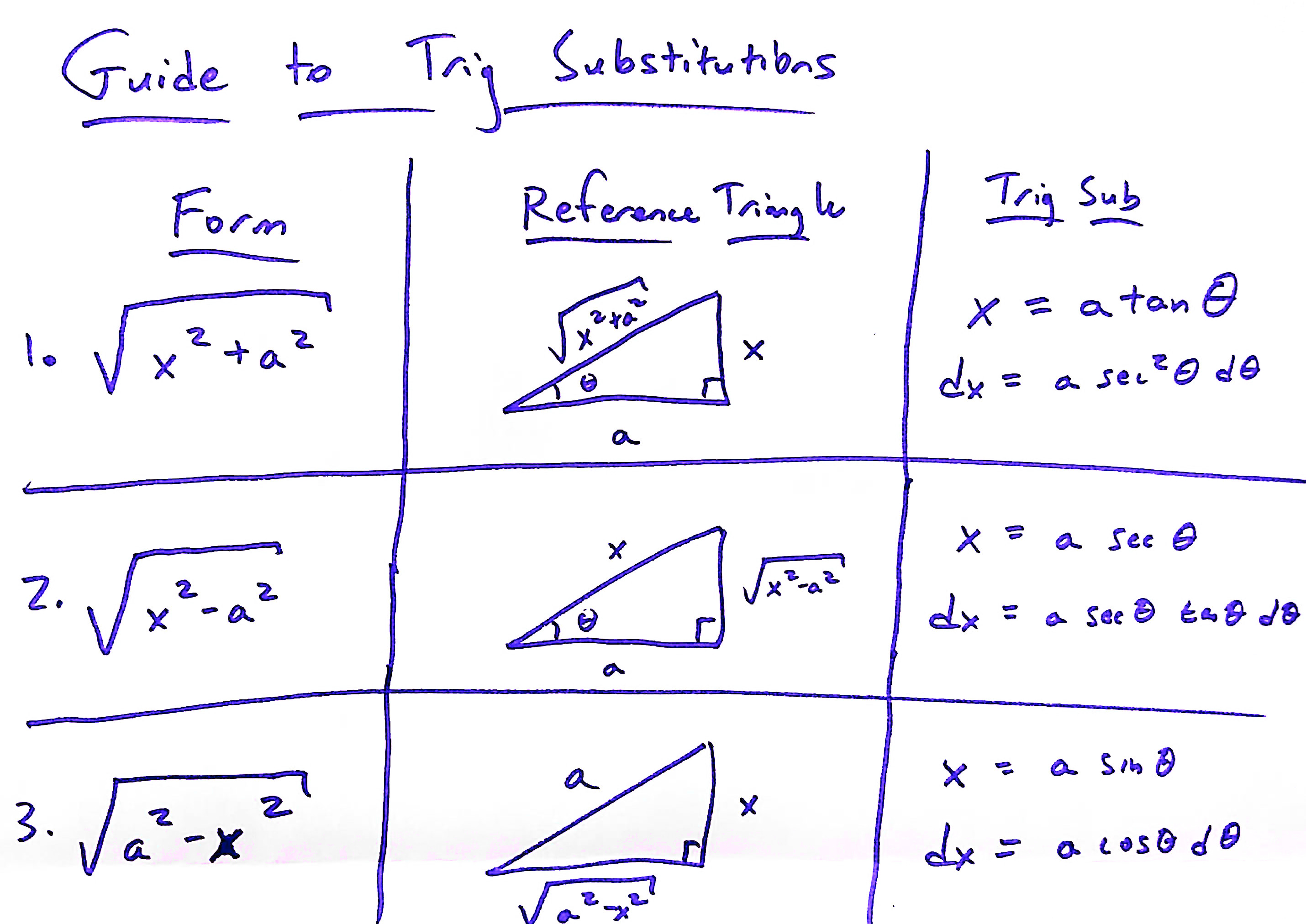
We used this table and both the half-angle formulas and the double angle formulas (which are on the formula sheet) to evaluate:
Then we introduced the partial fraction decomposition. This is an algebra technique that helps integrate rational functions.
Partial fractions works for any rational function where the degree of the numerator (top) is less than the degree of the denominator (bottom) and the denominator factors into linear (i.e., degree 1) factors that all have different roots.
If the degree of the numerator is bigger than or equal to the degree of the denominator, then use polynomial long division first.
We finished partial fractions with these examples:
Today we went over Homework 7. We also discussed this example:
Today we switched from integrals to limits. We will be using limits a lot in the next few weeks, so we need a fast way to compute them. One option that works frequently (but not always) is L’Hospital’s rule.
. (You can’t use L’Hospital’s rule here! Why not?)
.
. (Watch out, this one isn’t L’Hospital’s rule either!)
(Hint: The key to this one is to factor out the highest power of in the numerator & denominator).
This last example led us to talk about some short-cuts for limits as :
Remember that as , Logarithms are much smaller than Polynomials which are much smaller than Exponential functions.
Remember that higher degree polynomials grow much faster than lower degree ones. If the degrees are the same, then focus on the leading coefficients.
| Day | Section | Topic |
|---|---|---|
| Mon, Oct 9 | 7.5 | Improper integrals |
| Wed, Oct 11 | 7.5 | Comparison test for integrals |
| Thu, Oct 12 | Review | |
| Fri, Oct 13 | Midterm 2 |
Today we started with a very important limit which gives the Annual Percent Yield (APY) when you continuously compound interest payments with an Annual Percent Rate (APR) of . This limit is an indeterminant form , which can be converted to a L’Hospital’s rule by taking the natural logarithm of both sides. (https://youtu.be/Vy07ZncFZTQ)
After that example, we introduced improper integrals which are integrals involving infinity (either in the bounds, or because of a vertical asymptote). You deal with these just like any other definite integral, except you might have to calculate a limit to find the answer. We did several examples:
. This one turns out to just be 1, which illustrates a very important idea: The area under an infinite curve can still be finite!
. You could integrate this one without even realizing that it is technically an improper integral. But if you look at the graph, you’ll see why it counts as an improper integral.
.
If the value of the integral is a finite number, we say it converges. Otherwise, it diverges. An improper integral can diverge for two reasons. It might have infinite area, or there might not be one number that the area converges to which is why diverges. (https://youtu.be/ol9iqccSS1o)
We started with this warm-up problem:
For what values of and does converge? Does the constant matter?
We talked about the comparison test for integrals. If and are nonnegative functions and , then . This has two consequences:
If the bigger function has a finite integral, then the smaller integral must be finite too.
If the smaller function has an infinite integral, then so does the bigger one.
Compare the integrals and . One of these integrals is easy if you make the u-subsitution . Does that integral converge? What about the other integral? Can you use the comparison test here?
Use the comparison test to show that converges.
Does converge or diverge? (https://youtu.be/dvCeQFRHyww)
We didn’t have time for this last example, but it is a good one:
Here is a table to help keep the possible comparisons straight:
|
Smaller integral converges No info |
Smaller integral diverges So does the bigger |
|
Bigger integral converges So does the smaller |
Bigger integral diverges No info |
Today we went over Homework 8 and the review problems for the midterm tomorrow.
| Day | Section | Topic |
|---|---|---|
| Wed, Oct 18 | 8.1 | Areas and volumes by slices |
| Thu, Oct 19 | Review | |
| Fri, Oct 20 | 8.1 | Volumes by cylindrical shells |
Today we looked at two applications of integrals. First we looked at finding areas between curves. We did these two examples:
Find the area between and the line . (https://youtu.be/x4Yp-UF4vvI)
Find the area between and (https://youtu.be/9FBIbttJM1A).
Then we discussed how to use integrals to find volumes. We started with the problem of finding the volume of a pyramid, and came up with the central idea: that the volume of a solid is the integral of the areas of its cross sections.
If the cross sections are disks, this formula becomes .
Find the volume of a square pyramid if the base is 100 meters by 100 meters, and the height is 50 meters.
Find the volume of the solid formed by revolving the region between and the x-axis from to around the -axis. (https://youtu.be/X_2226aygDI)
Find the volume of a sphere with radius by revolving around the x-axis. (https://youtu.be/QLHJl2_aM5Q).
Today we went over some of the volume of revolution computations from Homework 9.
We also introduced the washers method. The formula for the washers method is:
We also reviewed the comparison test problems from Homework 8.
Another method for finding volumes of revolution is the shells method. Here is a video explanation of the shells method. We did these examples in class.
Find the volume of the region under , , revolved around the y-axis. (https://youtu.be/EX0rslFIL18)
Find the volume of the region under from to 1 revolved around the y-axis (https://youtu.be/cxj0OfZTWEo)
Find the volume of the region under from to revolved around they y-axis. (https://youtu.be/CiXME1u-oyU)
| Day | Section | Topic |
|---|---|---|
| Mon, Oct 23 | 8.2 | Length of a plane curve |
| Wed, Oct 25 | 8.6 | Force, work, and energy |
| Thu, Oct 26 | Review | |
| Fri, Oct 27 | no class |
Today we talked about how to find the length of a curve using integrals. There are two approaches. For a function with an explicit formula , use:
Arc length of from to . (https://youtu.be/OhISsmqv4_8)
Arc length of from to .
Write down an integral that represents the length of the parabola from to .
Use a Riemann sum with 100 rectangles to estimate the length of the parabola from the previous problem.
Today, we briefly talked about parametric equations and arc length by looking at Problem 4 on HW #10.
Then we introduced work and energy. For a variable force , work is the integral of force with respect to distance:
We did the following examples:
A force of 50 lbs. is needed to stretch a spring 5 inches longer than its natural length. How much work is required to stretch it 10 inches beyond its natural length? (https://youtu.be/TLw8xbmnY3c)
A spring has force where is the amount the spring is compressed (in meters) and the force is in Newtons. Find the work needed to compress the spring 1 meter?
If the compressed spring in the last problem pushes a 1 kg object along a slippery surface so that all of the potential energy of the spring is converted to kinetic energy of the object, then how fast will the object be moving after the spring pushes it? (Hint: recall that kinetic energy is .)
A 50 lb bucket will be raised from ground level to a height of 10 feet. The bucket is attached by a heavy chain (weighing one pound per foot) to a pulley 20 feet off the ground. How much work will it take to lift the bucket? (https://youtu.be/QA5mvSx5idE)
How much work is needed to pump water into a cylindrical tank that is 10 meters above the ground and is 3 meters tall with radius 1 meter? To solve this problem use the alternative formula for work: where is a the weight of a slice of water: and the weight density of water is 9800 Newtons per meter cubed.
We ran out of time before this example which is similar to one on the homework:
| Day | Section | Topic |
|---|---|---|
| Mon, Oct 30 | 10.0 | Infinite series: examples & patterns |
| Wed, Nov 1 | 10.1 | Geometric series |
| Thu, Nov 2 | Review | |
| Fri, Nov 3 | 10.2 | Convergence tests |
Today we talked about infinite series which is an infinitely long sum of numbers. This is very different than what we’ve been doing with integrals, so I would recommend reading the introduction to Chapter 10 in the book.
Before doing any calculations, we started with three example infinite series:
Zeno’s series .
Grandi’s series .
Harmonic series .
These examples led us to the following definition: an series converges if the limit of its partial sums is a finite number. Otherwise it diverges.
Then we talked about converting series that are written in term-by-term notation (like ) into summation notation with a -symbol. There are certain common patterns to watch out for:
Arithmetic patterns When you add the same amount each step. A formula for this pattern is where is the first term and is the step size.
Geometric patterns When you multiply by the same amount each step.
where is the first term and is the common ratio (the common amount you multiply by).
Alternating patterns If the terms alternate between positive and negative, you can write a formula for this by including a factor of either depending on which way the series alternates.
We did the following examples (since these aren’t in most textbooks, I’ve included solutions too.).
We ran out of time and didn’t do example 2 above. We’ll do that at the start of class on Wednesday.
We started with this warm up problem:
Some important things to know include the fact that , and that expressions with factorials in both the numerator and denominator can be simplified by canceling the factors inside. For example, simplify the following expressions (without a calculator):
.
.
.
Then we talked about geometric series, which have the formula:
as long as the common ratio satisfies . Geometric series diverge if , which means the infinite sum does not make sense.
We proved that a geometric series converges when . Here is a video that goes over that proof. Then we did more examples of recognizing patterns.
We did the following examples in class:
What is the sum of ?
Find the sum of . (https://youtu.be/uebsyi1Jigw)
If the sides of the outer square are both 2 meters long, find the total area of the darker squares:
We reviewed Homework 11. We also talked about why the formula for geometric series is correct and we did these examples:
Convert the repeating decimal to a geometric series and then a reduced fraction.
If , what is ?
What would happen if you integrated the previous answer? This question led us to find a formula for !
Today we talked about four different convergence tests for infinite series:
Here is a simple idea that is pretty obvious: an infinite sum cannot converge unless the terms in the sum are getting closer and closer to zero. That’s one reason that Grandi’s series () cannot converge. This simple idea is called the divergence test. Unfortunately, you can’t turn it around and say that a series with terms getting closer & closer to zero will converge. That isn’t true.
Integral Test. A series with positive terms that are given by a decreasing function converges if and only if the integral converges.
A p-series is a series of the form:
The special case when is the harmonic series. We used the integral test to show that p-series converge if and they diverge otherwise. This is called the p-test for infinite series and it is exactly the same as the p-test for integrals.
We finished by talking about the comparison test which works the same for infinite series as it does for integrals.
| Day | Section | Topic |
|---|---|---|
| Mon, Nov 6 | 10.3 | Alternating series |
| Wed, Nov 8 | 10.3 | The ratio test |
| Thu, Nov 9 | Review | |
| Fri, Nov 10 | 10.4 | The Taylor series for ex, sin x, & cos x |
Start with this example which we did not do in class on Friday.
We wrote down an infinite series for and we integrated to get an infinite series for .
What does the series above become when ? Does the series converge? How can you tell?
Use the series above to approximate . How accurate is it when you use terms?
After that example we introduced alternating series and the
Alternating Series Test. If is positive and decreasing, then the series converges if and only if . If an alternating series meets the conditions of the alternating series test, then you can estimate the error in a partial sum using the alternating series error formula:
For each of the following, write out the first 4 terms of the alternating series, and determine whether it converges or diverges. How many terms would you need to make the error less than ?
Today we defined absolute convergence and conditional convergence for infinite series: Then we introduced
converges absolutely if converges.
converges conditionally if diverges but converges.
Show that the alternating harmonic series converges conditionally.
Show that converges absolutely.
Then we introduced the ratio test for absolute convergence. For any infinite series, ,
Use the ratio test to determine whether the following series converge.
.
Why doesn’t the ratio test work on this infinite series ? This turned out to be a pretty ugly limit when we did it in class. It’s definitely a good example of where not to use the ratio test!
Today we reviewed homework 12. We also looked at the following example.
Definition. A power series is an infinite series: where
Fact 1. Every power series has an interval of -values where it converges, called the interval of convergence. The interval is always centered at the center and has a radius of convergence that is the distance from to either endpoint.
Fact 2. When a power series converges, it converges to a function of : and the coefficients of the series are where is the -th derivative of .
We used Fact 2 to find a power series for that is centered at .
| Day | Section | Topic |
|---|---|---|
| Mon, Nov 13 | 10.4 | Taylor series - con’d |
| Wed, Nov 15 | 10.5 | Power series |
| Thu, Nov 16 | Review | |
| Fri, Nov 17 | 10.5 | Applications of Taylor series |
| Mon, Nov 20 | Midterm 3 |
Today we looked at more examples of power/Taylor series. We focused mostly on Maclaurin series which are Taylor series centered at zero. We also defined Taylor polynomials which are the partial sums of Taylor series.
Find the Maclaurin series for by making a table of derivatives and finding the pattern. (https://youtu.be/8dMLK2Wueaw)
Find the interval and radius of convergence for the Maclaurin series for by using the ratio test.
According to the Maclaurin series, Estimate the worst case error in this approximation.
Find the Maclaurin series for by making a table of derivatives and finding the pattern. (https://youtu.be/JYQqml4-4q4)
Find the Taylor series for centered at .
Today we talked about easier ways to find Taylor and Maclaurin series. We started with this handout:
Find a Maclaurin series for by starting with the series for and dividing every term by . (https://youtu.be/SFRKtSCVRNs)
Find the antiderivative of . (https://youtu.be/SFRKtSCVRNs)
Find an infinite series for the definite integral .
How many terms of that infinite series would you need to approximate the answer accurate to eight decimal places (i.e., with error less than )?
Find a Maclaurin series for by substituting in place of in the Maclaurin series for . (https://youtu.be/x5J01OR_LSo)
What is the series for the derivative? Is it the same if you do the chain rule first before finding the Maclaurin series?
Multiply the Maclaurin series for and to find the 4th degree Maclaurin polynomial for . (https://youtu.be/oIrp4dyo6jE)
Today we reviewed the problems on the midterm 3 review sheet and on homework 13. We also voted to postpone the midterm until Monday instead of having it on Friday.
Today we talked about applications of Taylor series. We looked at these examples:
. What is the interval of convergence for ? Show that in the interval of convergence. Use that to find a formula for as an infinite series.
What is the number as an infinite series?
Why can’t you use the Maclaurin series for to find by substituting into the Maclaurin series? What happens if you substitute instead?
Calculate the impossible integral using a power series.
Calculate these two limits by using the Maclaurin series for cosine:
| Day | Section | Topic |
|---|---|---|
| Mon, Nov 27 | 10.5 | Taylor remainder formula |
| Wed, Nov 29 | Presentations | |
| Thu, Nov 30 | Presentations | |
| Fri, Dec 1 | Presentations | |
| Mon, Dec 4 | Review |
A lot of applications of Taylor series lead to alternating series which are nice because they come with a built in error estimate. But what about applications that do not alternate?
Taylor Remainder Theorem. For any function that is differentiable times on the interval from to , there is a number between and such that the gap between the function and its th degree Taylor polynomial centered at is: We call this gap the remainder .
Think of the Taylor polynomial as the approximation, and the remainder as the error.
Estimate the error in using the 2nd degree Maclaurin polynomial for to estimate . (https://youtu.be/pZBRc5uegEs)
Estimate using a 2nd degree Taylor polynomial. Include an estimate for the error.
After these examples, we gave a quick refresh on the Mean Value Theorem. Then we observed that you can obtain Taylor’s remainder theorem by starting with the mean value theorem for :
for some between and . Then multiply both sides by and integrate with respect to a total of times. If you are careful with your integration constants, then you get Taylor’s remainder theorem.